Technical Terms of Drone
テクニカルターム

Ll

Lift
揚力

揚力/lift は 流体/液体や気体 中を移動もしくは流れにさらされた物体が 流体から受ける力/流体力 の成分の一つで 物体の進行方向や流れが物体に向かう方向に対して垂直に働く力を指す
一方 進行方向に平行する成分は抗力と呼ぶ
そしてこの揚力と抗力の比を揚抗比と呼ぶ
通常 物体と流体に相対速度があるときに発生する力/動的揚力 のみを指し 物体が静止していてもはたらく力である浮力/静的揚力 は含まない
揚力の応用例として 重力と反対方向へ揚力を生じさせることで飛行機の巡航時に垂直方向の釣り合いをとる

概要

空気や水といった流体の中に物体があり 物体とその周囲の流体との間に相対速度がある時
物体とともに移動する視点について 主流 および 主流速度 が定義できる
このとき その物体は流体との接触面を介して周囲流体と力を及ぼし合う
すなわち物体から受ける力によって周囲の流れは変化し 同時に物体は流れから力を受ける
物体が主流方向に受ける力を抗力と呼ぶ
物体が主流速度ベクトルに対して対称な形状である場合 主流に垂直な力の成分は生じないが 非対称な形状の場合は 物体は主流方向からそれた斜めの方向に力を受け 主流に垂直な力の成分を揚力と呼ぶ
それ自体の形状が上下対称であっても 正の迎角がある場合は、主流に対して非対称であり 揚力を発生する
例えば 単純な平板の 形状/上下対称の翼型がある→凧や帆

カルマン渦と揚力

物体後流にはカルマン渦と呼ばれる渦列が周期的に発生し 流体力は振動していることが多い

このため 回転なし迎角なしで正味の揚力がゼロとされる形状であっても瞬時の揚力は生じている事がある

翼表面上の圧力
流体が物体におよぼす力は 物体表面の応力 すなわち圧力と摩擦を表面すべてで積算した量である
ただし 揚力は圧力だけで説明できると考えられており 圧力場を物体表面で積算した合力が揚力である したがって揚力が上向きのときに物体表面の圧力分布をみると物体上側で低圧/下側で高圧の傾向がある

速度場

翼表面圧力が上部で低圧である以上 対応する速度をみると物体の上側で高速下側で低速の分布である このため翼型境界線で循環を見積もると有限の値をとる 物体に揚力が働いているとき 揚力に対する反作用として揚力と逆向きの運動が物体周囲の流体のどこかにかならず生じる

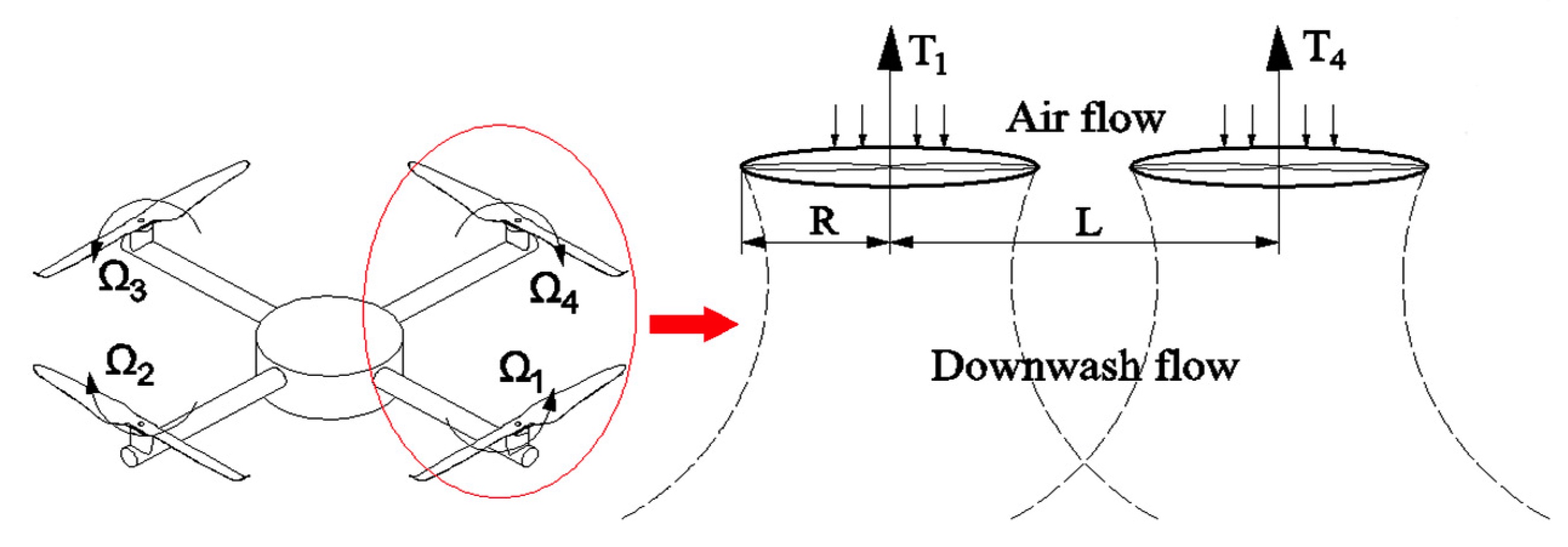
翼体の上背面から翼後端の後方にかけて顕著な下向きの流れは 主に航空機工学の分野において「ダウンウォッシュ」と呼ばれる

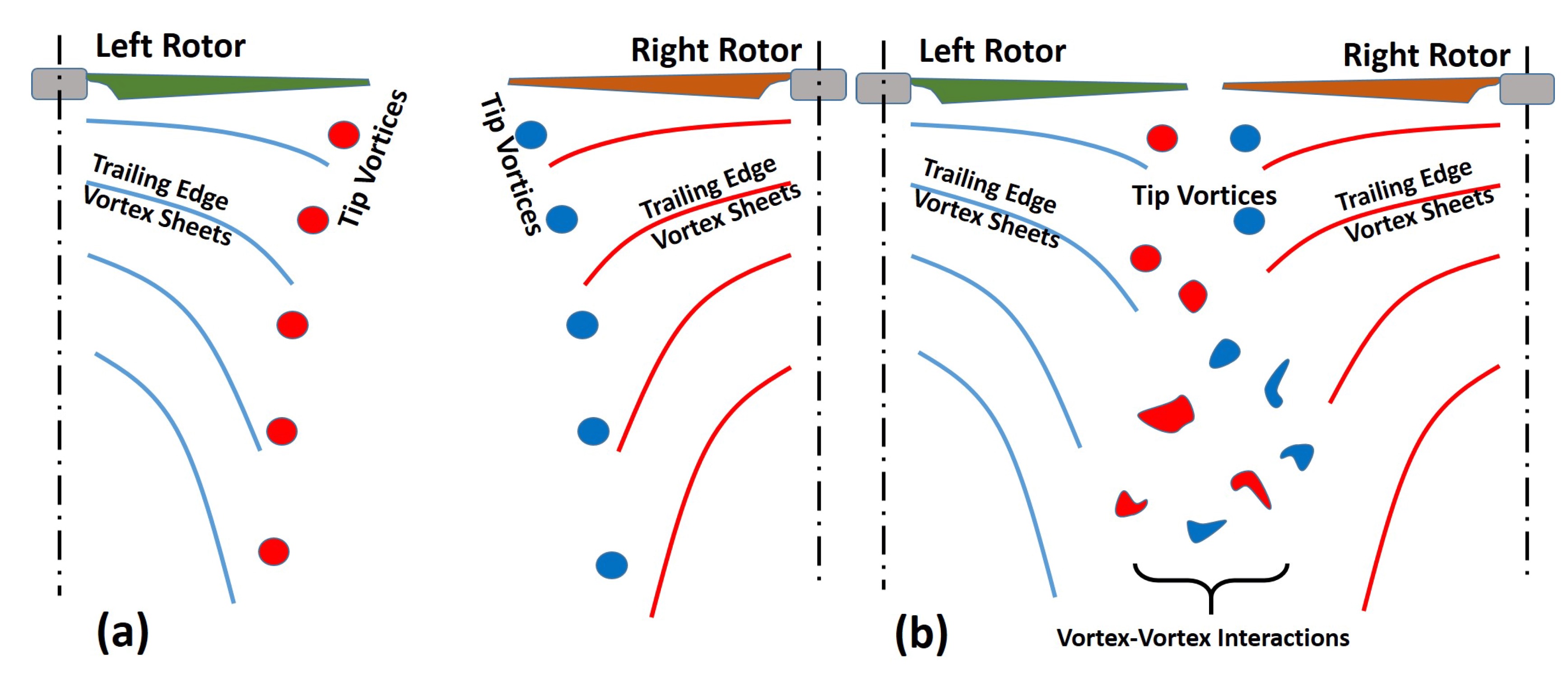
翼まわりの渦

ダウンウォッシュは翼後縁が横切った矩形状領域に生じる
この矩形状の線は下降流と上昇流の境であり せん断すなわち渦度が集中し 渦が生じる

ただし矩形の前方側は翼体によって仕切られているため翼まわりの循環が渦の代わりとなる
ダウンウォッシュは翼後縁と２つの翼端渦と出発渦とで囲まれた形となる

ダウンフォース

「揚力」は字義どおりに重力の反対方向に働くとは限らない
飛行機の場合 機体の姿勢に合わせて機体からみた上方向に働く力を揚力とする
レーシングカー等では下向き揚力をダウンフォースと呼び表すことがある
帆船の帆に働く揚力はほぼ水平方向を向いている
風車やタービンでは周方向
プロペラでは回転軸方向がおおよその揚力の向きとなる

揚力を利用する例

揚力の利用例として
植物の種子
昆虫の翅
水性動物のヒレ
鳥類の翼
凧
飛行機の固定翼
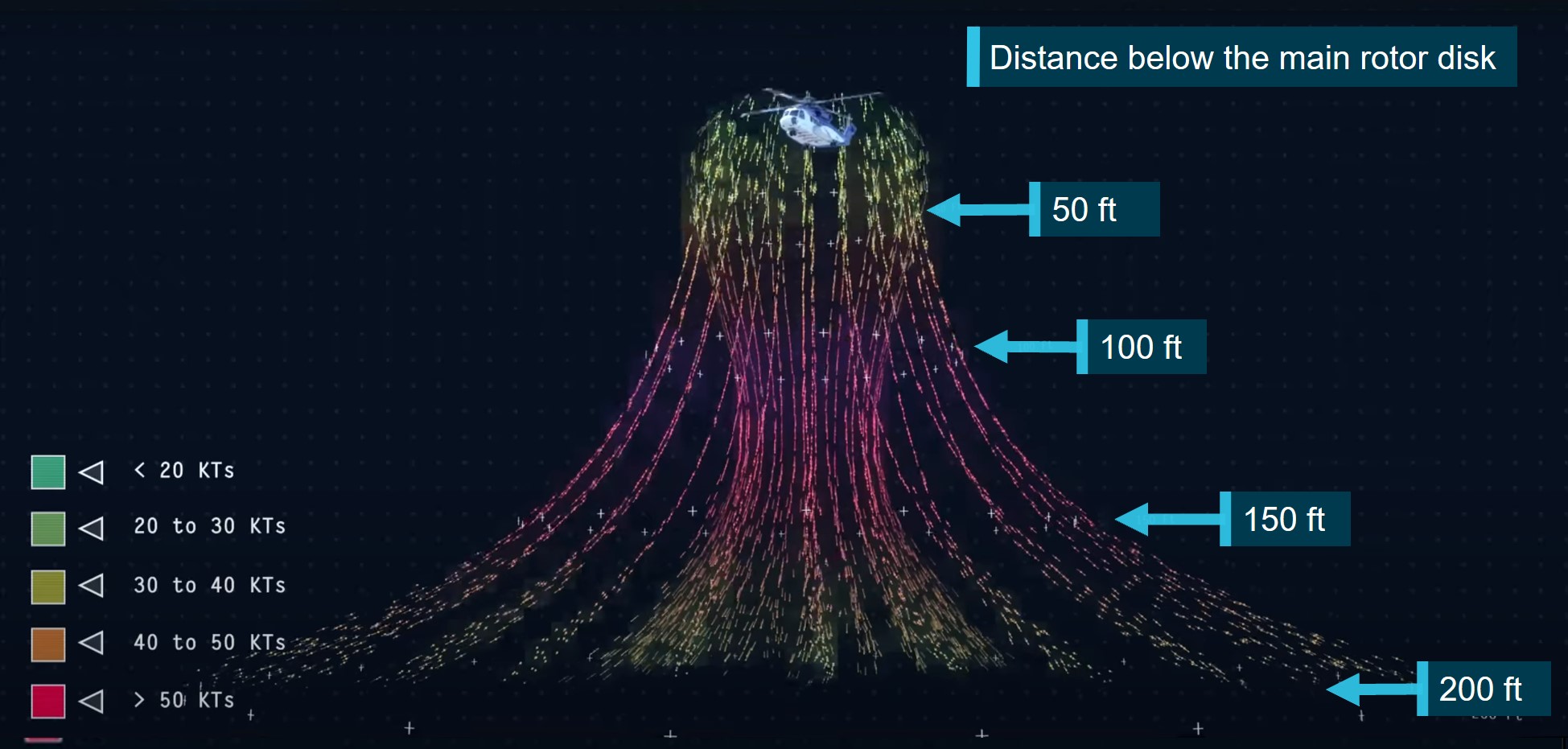
ヘリコプターの回転翼
水中翼船の水中翼
船舶の帆/縦翼 と 舵
櫂
プロペラ
ファン
タービン
などがある

スポーツ

卓球/野球をはじめとする球技では物体の回転によって生じる揚力が利用される円柱または球の回転体が 粘性を有する流体中を一定速度で移動している または一様流中に置かれた場合 円柱または球が回転している状態において 回転体の回転軸ベクトルと流体との相対速度ベクトルに垂直の方向に力が発生する
その大きさは 流体の密度/回転体と流体との相対速度および回転体の回転速度に比例する 水泳では揚力を強調した腕の動きを取ると長時間楽に泳げる

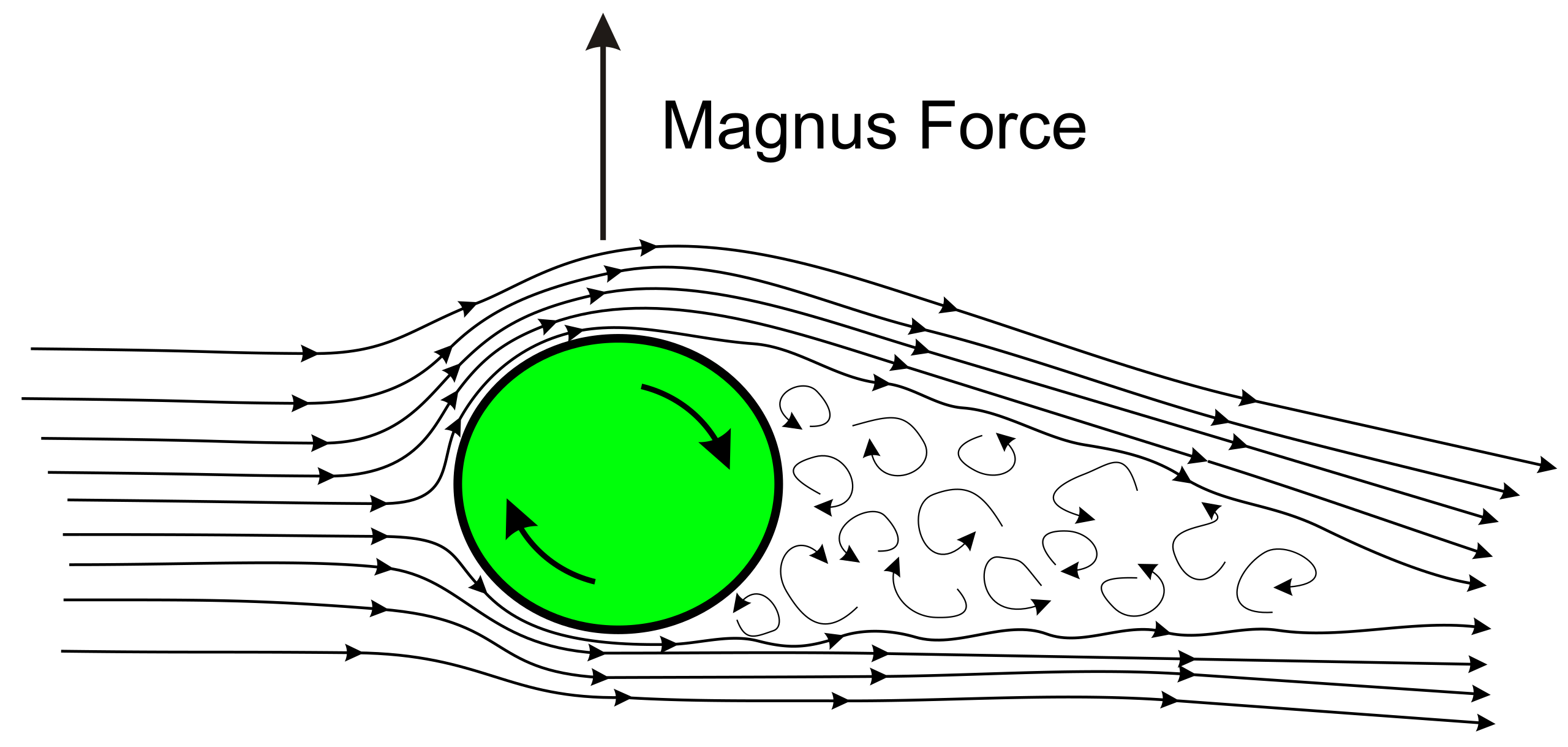
マグヌス効果/Magnus effect は 回転しながら進む物体にその進行方向に対して垂直の力/揚力 が働く現象を言う
マグナス効果とも呼ばれる
ベンジャミン・ロビンス/Benjamin Robins によって観察された小銃から発射される球形の弾丸が曲がることを説明するにあたって 1852年にドイツの科学者ハインリヒ・グスタフ・マグヌスによってはじめて認識された

円柱または球の回転体が 粘性を有する流体中を一定速度で移動している または一様流中に置かれた場合 円柱または球が回転している状態において 回転体の回転軸ベクトルと流体との相対速度ベクトルに垂直の方向に力が発生する
その大きさは 流体の密度/回転体と流体との相対速度 および回転体の回転速度に比例する

流線の密度が疎な部分には カルマン渦に代表される渦の形成が容易になる
これは時間的周期性を持ち円柱断面を仮定した場合上にも下にも揚力を形成し 流体関連振動となる
この原因は渦の離脱による圧力低下が原因であり それを非対称に設計したジューコフスキー的形状においてはカルマン渦の発生が上下非対称になるため揚力が発生する
そのため そういう周期的圧力欠損に頼るため 小さな航空機では振動が激しくなる

揚力係数

正味動圧と揚力の比/無次元数 ある
物体の形状/進行方向/迎角/流体の物性/流速/レイノルズ数/マッハ数 などによって変化する
翼や縦帆などでは 迎角がある程度に小さいときには迎角に比例して変化する
迎角の絶対値が大きくなると 物体表面から流れが剥離して揚力係数の絶対値は小さくなり 抗力が急激に増大する[^ ]この現象を**失速**と呼ぶ
翼体の高度が小さく地面や水面の近くを飛ぶときは高高度に比べて揚力係数は大きくなる
これを 地面効果/Ground Effect という
ある形状に対する揚力係数は 実際に揚力を測定/数値シミュレーションで求めてもよい
実務上は 形状とレイノルズ数についてそれぞれ同一とみなされる場合には揚力係数も同値とすることがある

航空機の翼/翼型
翼型とは翼の断面形状のこと
基本的には 前端側が丸く後端側が尖ったいわゆる「涙滴形」やそれを湾曲させひずませた形状である
航空機の場合は翼内部ボリュームを大きくすることも要求され 翼型設計に影響する
運用時の迎え角が一定でないことを前提に 前縁部近傍は剥離を防ぐために丸く 曲率を小さくする
翼下面の流れが後端部で翼から離れるために後端は曲率を大きく 尖らせる
翼断面の図としてよく見られる形状は 上面側のほうが翼が膨らんでおり 下面側はやや平らになっている
1960年代以降広く採用されているスーパークリティカル翼は 低抗力と湾曲とを両立させている
超音速用途では前端も尖らせた形状が普通である

航空機の翼/翼と迎角 航空機の翼は迎角をつけて機体に固定されている
多くの旅客機は巡航状態でさらに機体を1-2度上向きに傾け全体の抗力が最小となるよう設計されている
揚力が低速で不足する際 もしくは上昇時は 機体をさらに大きく上向きへ傾ける必要がある
離着陸時にはフラップでさらに揚力を増やす

航空機の翼/プロペラ
一方 プロペラ機のプロペラにも同様のことが成り立つが 翼とは事情が異なる
可変ピッチ機構を持つプロペラの場合は 離着陸時や最高速度域ではピッチ つまり回転方向に対する迎角を小さくし 一方でプロペラの回転数を上げる
ピッチ角を小さくし抗力を小さくして プロペラの能率を最大限に高めるためである
一方で巡航時にはピッチ角を大きく取り エンジンの回転数を下げる
プロペラそれ自体の効率を考えれば抗力が大きくなる分悪化するものの エンジンの回転数を下げることにより燃費効率が上がる効果のほうがより大きいからである
マルチローターでないヘリコプターにおいては ローター/回転翼 の角度調整は極めて重要である
ヘリコプターが前進する時 回転するローターブレードの片方は機体と同じ方向に回転し大気との相対速度が大きく もう片方は機体と逆方向に回転するため相対速度が小さい
よってローターブレードの左右で揚力の差が生じる
よって回転軸固定のシングルローターヘリコプターには左右のローターブレードが発生する揚力を等しくするため 迎角を調整する装置が必要不可欠となる

原理に関する誤解説の例

飛行機の揚力については既に等角写像を用いた理論が構築されており厳密な計算が可能である一方 原理については完全に解明されたと言い切れない部分がある
飛行機がなぜ飛ぶのか未だに分かっていない といった言い方がされ 科学啓蒙書や航空工学の専門家の書物などでもこのような説明が書いてある
本当は 飛行機がなぜ飛べるのかは分かっているのに 一般向けの文書には明らかに誤りを含んだ解説がある

原理に関する誤解説の例/圧力と反作用の関係
揚力の解説の中には 反作用に言及が無いものや圧力分布に言及が無いといった簡易なものがある
なかには反作用と圧力分布の一方を否定するものがあるが 圧力差こそが反作用であり 当に誤解である

原理に関する誤解説の例/圧力と反作用の関係/揚力は圧力差であり反作用はないという主張
これは 翼を動かしたときに生じる圧力差 との区別しづらい状況でしばしば陥る誤解である
翼面に垂直に働く駆動力は圧力場であり これは流体から翼への作用である
このとき 作用反作用の法則の通り 流体側は正負逆の力を受ける
揚力を議論しているときの流体の圧力差とは 主流中の翼体の運動によるものである
それが抗力と揚力の反作用でないなら 別の要因があり追加の説明が必要である

原理に関する誤解説の例/圧力と反作用の関係/揚力は圧力によるものではないという主張
なら何の力によるかが示されていない
反作用は力の種類ではない
全ての力は基本相互作用が基になっているが それまでの間か示されていない
車両は路面からの反作用で走るが 車輪と路面との摩擦力は関係ない というようなものである
翼の上下のように非対称でも圧力が同じというのは 流体動力学の基本のベルヌーイの定理に反する

原理に関する誤解説の例/同着説/等時間通過説
翼の上下の圧力差の発生原因において 次のような説明がなされることがある
翼は下面より上面の膨らみのほうが大きい
翼の前縁で上下に別れた気流は 後縁で同着する
よって より距離の長い上面の方が流れが速く ベルヌーイの定理によって気圧が下がり 揚力が発生する
しかし 翼の前縁で上下に別れた気流は 後縁で同着する という部分は誤りである
実際には同着しておらず 下側の方が時間がかかり遅れる
そもそもこの発生原因では 背面飛行や上下対称の翼型の揚力の説明ができていない

原理に関する誤解説の例/抗力と揚力の合力
流れの中にある平板が受ける力は 現実には斜めの力であり 抗力と揚力は水平方向/垂直方向への分力に過ぎない
抗力と揚力は 物体が流体から受ける正味の力の分力である
その元々の正味の流体力の呼称に困り 揚力と抗力の合力 といわれることがある
…揚力と抗力が生じ 翼はその合力を受ける という表現も見られる
これは定義の循環である
揚抗比で説明している通り 揚力だけが独立して生じることは無い

.. .. Under Construction .. ..

.. to be continued ..

Mm

.. .. Under Construction .. ..